La Sezione Aurea

La sezione aurea è un rapporto geometrico e numerico proporzionale che intercorre fra due parti nelle quali un segmento è diviso.

E’ una proporzione geometrica che fin dall’antichità classica è stata usata, in architettura e nei manufatti, poiché è considerata elemento di armonia proporzionale, ed è stata ricavata dall’armonia proporzionale che si trova in tanti elementi della natura.

Dato un segmento (AC), si ottiene una sezione aurea quando il tratto più corto (BC) sta al tratto più lungo (AB) come il tratto più lungo (AB) sta al segmento intero (AC).

In sintesi la proporzione è così espressa:

BC : AB = AB : AC

Come si può ottenere graficamente la sezione aurea?

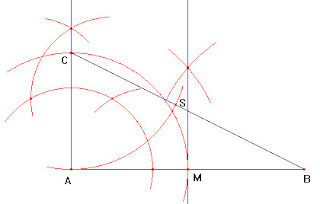
Disegna un segmento di qualsiasi lunghezza.

Costruisci la perpendicolare all'estremo A

Costruisci la perpendicolare al punto medio M

Punta il compasso in A con apertura AM e traccia un arco

che taglia la perpendicolare in C

Unisci CB

Punta il compasso in C con apertura CA e traccia un arco che taglia CB in S

Punta il compasso in B con apertura BS e traccia un arco che taglia AB in R.

Il punto R corrisponde alla sezione aurea:

AB : BR = BR : AR

Sei in grado di calcolare qual é il valore del rapporto AB/BR o BR/AR?

e il valore del rapporto BR/AB o AR/BR?

Se scrivi la serie di Fibonacci (la serie in cui ogni termine si ottiene dalla somma dei due precedenti 1 1 2 3 5 8 13 ecc.) e consideri due termini consecutivi (esclusi i primi) scrivendoli in forma frazionaria (es. 8/13 ; 13/8), calcolando i rapporti, noti qualche analogia con la sezione aurea?

Costruisci una serie di quadrati, secondo lo schema, rispettando la serie di Fibonacci.

In questo modo si creerà una successione di rettangoli sempre più vicini a quello aureo, ma è bene precisare che sarà sempre una approssimazione che non diventerà mai esatta: perché il rapporto aureo è un numero irrazionale, il che fa dei lati del rettangolo in esame due grandezze incommensurabili, per le quali, cioè, non esiste un sottomultiplo comune; come si vede dall'immagine il procedimento dei quadrati di Fibonacci crea invece lati sempre esprimibili tramite numeri interi, il che significa che il loro rapporto sarà sempre un numero razionale.

(da Wikipedia)