A volte si ha la necessità di disegnare un oggetto che nella realtà ha dimensioni troppo grandi per essere contenuto nel foglio (pensa ad una casa, a un'automobile, a un mobile) oppure troppo piccole (un ruotismo di un orologio, o di un motore) per essere rappresentato in modo preciso. Ci troviamo nella necessità di disegnare l'oggetto in dimensioni ridotte, nel primo caso, o ingrandite, nel secondo, mantenendo però inalterate tutte le proporzioni tra altezza, larghezza e profondità.
Le dimensioni dei nostri disegni artistici sono quasi sempre diverse da quelle reali e fino ad ora non ci siamo preoccupati di precisare le misure reali effettive, accanto alle figure.
Le dimensioni dei nostri disegni artistici sono quasi sempre diverse da quelle reali e fino ad ora non ci siamo preoccupati di precisare le misure reali effettive, accanto alle figure.
In tecnologia, quando si rappresentano gli oggetti tecnici, si deve indicare quante volte il disegno è "più piccolo" o "più grande" delle dimensioni reali.
Utilizziamo come unità di misura:
Utilizziamo come unità di misura:
Se disegniamo il quadrato A
di lato 3 q
e poi ne vogliamo disegnare uno B, grande il doppio,
possiamo osservare che il perimetro è raddoppiato,
(perimetro A = 12q
perimetro B = 24q)
ma l'area è quadruplicata.
(area A = 9 Q
area B = 36 Q)
Ora ci sorge un dubbio: il quadrato B è doppio o quadruplo di A?
E' doppio rispetto al perimetro e quadruplo rispetto all'area.
Noi dobbiamo raddoppiare il perimetro o l'area?
Proviamo a disegnare un quadrato di area doppia di A (18 Q)
Come puoi vedere l'area di E è 16 Q e l'area di F 25 Q e quindi né l'uno né l'altro sono corretti.
Quanto misura il lato del quadrato di area doppia di A?
Se hai studiato la geometria saprai che per calcolare il lato basta estrarre la radice quadrata dell'area.
Il quadrato G ha area doppia di A.
Raddoppiando l'area delle figure occorre eseguire calcoli più o meno complessi per ricavare le dimensioni dei lati e pertanto si preferisce lavorare sulle misure dei lati o perimetro.
Ora ci potrebbe sorgere una curiosità: se noi raddoppiamo la misura dei lati (perimetro), l'area quadruplica sempre?
area = 13 Q
Disegniamo la figura con i lati di lunghezza doppia
perimetro = 40 q
area = 52 Q
Effettivamente raddoppiando la misura dei lati l'area quadruplica.
Facciamo ancora una prova.
area = 11 Q
Disegniamo la figura con i lati di misura doppia (mantenendo, nell'ordine, gli stessi angoli).
area = 44 Q
Anche in questo caso raddoppiando la misura dei lati l'area quadruplica.
Possiamo affermare (fino a prova contraria) che, in una figura geometrica, raddoppiando la lunghezza dei lati e mantenendo gli stessi angoli, l'area quadruplica.
E se triplichiamo le misure dei lati?
Consideriamo il quadrato e l'altra figura irregolare
area quadrato = 4 Q
area figura = 3 Q
Triplichiamo la lunghezza dei lati:
area quadrato = 36 Q
area figura = 27 Q
Triplicando la lunghezza dei lati, l'area diventa nove volte più grande.
E se quadruplichiamo le misure dei lati?
area = 3 Q
area = 48 Q
Quadruplicando la lunghezza dei lati e mantenendo gli stessi angoli, l'area diventa 16 volte più grande.
Riassumendo:
Qual è la regola che stabilisce il rapporto area-perimetro nelle figure simili?
Se hai studiato le potenze, vedi che i numeri 4 - 9 - 16 sono il numero di volte che si è moltiplicato il perimetro, elevato 2.
Se noi moltiplicassimo la lunghezza dei lati per 14, l'area della figura simile sarebbe:
Come facciamo ad indicare che il disegno è ingrandito o ridotto rispetto alle dimensioni reali?
Utilizziamo la dicitura:
SCALA numero : numero
(il segno ":" si legge "a")
Generalmente uno dei due "numero" è l'1
SCALA 1 : 1
Significa che il disegno ha le stesse dimensioni dell'oggetto reale.
SCALA 1 : numero (intero)
es. SCALA 1 : 25
Significa che il disegno è ridotto rispetto alle dimensioni reali, di tante volte quante ne indica il "numero" (le sue dimensioni sono state divise per il "numero").
SCALA numero (intero) : 1
es. SCALA 8 : 1
Significa che il disegno è ingrandito rispetto alle dimensioni reali, di tante volte quante ne indica il "numero" (le sue dimensioni sono state moltiplicate per il "numero").
* * *
Esempio 1
Consideriamo la figura:
la Scala 1:1 indica che le misure dei lati sono reali.
Se vogliamo rappresentarla in Scala 1:2 dobbiamo dividere per 2 le lunghezze "reali" dei lati.
Per disegnarla in Scala 2:1 dobbiamo moltiplicare per due le lunghezze "reali" dei lati.
Esempio 2
Anche in questo caso abbiamo una figura in Scala 1:1, con le dimensioni uguali alla realtà.
Come vedi ci sono delle linee inclinate, ma particolari, perché sono tutte diagonali dei quadretti.
La diagonale di un quadretto è il segmento che unisce due vertici non consecutivi (opposti)
Se devi ingrandire una figura, gli angoli non devono cambiare e di conseguenza le diagonali continuano ad essere diagonali, più lunghe o più corte a seconda della scala.
Esempio 3
Questa figura, in Scala 1:1, ha i lati inclinati che non sono diagonali dei quadretti.
Ingrandendo o riducendo le dimensioni, come si fa a mantenere esattamente l'inclinazione?
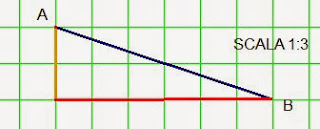
Pensa di doverti spostare da A a B, seguendo un percorso orizzontale e verticale. Da A puoi raggiungere B percorrendo A-1 e poi 1-B oppure A-2 poi 2-B. Se devi raddoppiare AB mantenendo l'inclinazione raddoppierai i tratti (orizzontale e verticale).
Applichiamo questo metodo per modificare la Scala della figura.
Esempio 4
La figura non è rappresentata con le misure reali, ma ridotte di 6 volte (divise per 6).
Se vuoi disegnarla in Scala 1:12 devi ricavare le misure "reali" e poi dividerle per 12.
Il percorso AB è composto da un quadretto verticale e 3 orizzontali, in Scala 1:6.
Per passare alla Scala 1:12 occorre prima passare alle misure "reali" moltiplicando per 6 e poi dividendo per 12.
1 x 6 = 6; 6 : 12 = 0,5
3 x 6 = 18; 18 : 12 = 1,5
Per disegnare AB in Scala 1:3 occorre ottenere le misure "reali" moltiplicando per 6 e poi dividendo per 3.
1 x 6 = 6; 6 : 3 = 2
3 x 6 = 18; 18 : 3 = 6
La figura completa:
Esercizio
Disegna la figura in Scala 1:2
Puoi disegnare la figura in Scala 1:1 (moltiplicando le misure per 3) e poi in Scala 1:2 dividendo le misure "reali" per 2.
Oppure puoi disegnare subito la figura in Scala 1:2 moltiplicando le misure della Scala 1:3 per 3 e poi dividendole per 2.
Esercizio
In questo caso la figura è più grande della realtà di 6 volte e pertanto le misure "reali" si ottengono dividendo per 6 quelle del disegno.
Disegna la figura in Scala 3:1
Per ottenere le misure della Scala 3:1 occorre dividere le misure della Scala_1:6 per 6 e poi moltiplicarle per 3.
Per ottenere le misure in Scala 9:1 occorre dividere le misure della Scala_6:1 per 6 e poi moltiplicarle per 9.
Esercizio 1
Esercizio 2
Esercizio 3
Per evitare errori, se possibile, disegna sempre la scala 1:1
Correzione compito: esercizio 1
Disegna in scala 3 : 1
esercizio 2
disegna in scala 1 : 4
Esercizio
disegna in scala 1 : 8
(Il disegno in scala 1 : 1 occupa uno spazio troppo grande e non puoi riprodurlo sul foglio di quaderno. Occorre pertanto effettuare un ragionamento per ottenere le dimensioni in Scala 1 : 8.
Se il corvo in scala 1:4 ha l'altezza di 9 q, il corvo "reale" ha l'altezza di 36 q.
In scala 1:8 le misure si ottengono dividendo per 8 le misure reali e quindi l'altezza è 36:8 = 4,5 q.
Conclusione del ragionamento: le misure in scala 1:8 sono la metà di quelle in scala 1:4.)
Esercizio
Disegna in scala 1 : 10
Come nel caso precedente non puoi disegnare lo squalo in scala 1:1.
Il disegno in scala 1:10 è più grande di quello in scala 1:20.
Lo squalo in scala 1:1 è alto 120 quadretti; in scala 1:20 è alto 120:20=6 quadretti; in scala 1:10 è alto 120:10=12 quadretti.
Pertanto in scala 1:10 le dimensioni sono doppie rispetto alla scala 1:20.





























































uffa devo solo ricavare un misura da una inclinazione
RispondiEliminaNon si capisce niente
RispondiEliminaNon si capisce assolutamente niente
RispondiElimina