Abbiamo visto (ingrandimenti e riduzioni) che i disegni si possono riprodurre in scala e che la riduzione o l'ingrandimento non alterano le proporzioni.
Consideriamo ora la possibilità di effettuare, nello stesso disegno, due diverse scale di proporzione: una per le dimensioni verticali e una per le dimensioni orizzontali.
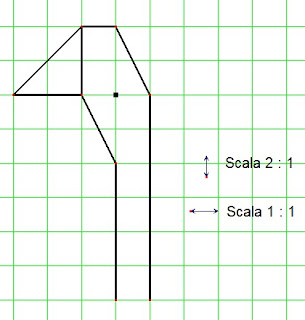
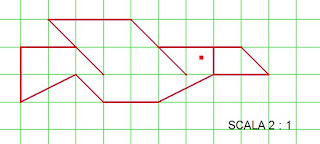
Se tutte le linee verticali restano della stessa lunghezza (Scala 1 : 1) e tutte le linee orizzontali raddoppiano (Scala 2 : 1)
otteniamo una figura DEFORMATA (stiramento orizzontale).
Se, invece, tutte le linee orizzontali restano invariate (Scala 1 : 1) e quelle verticali triplicano (Scala 3 : 1)
otteniamo una figura "stirata verticalmente"
E' necessario indicare, vicino alla figura, le due diverse Scale: quella utilizzata per le misure verticali e quella utilizzata per le misure orizzontali.
Naturalmente si può utilizzare qualsiasi Scala per le dimensioni verticali ed orizzontali.
E le linee oblique?
Devi pensare ad A come punto di partenza e B punto di arrivo. Per andare da A a B puoi percorrere la linea obliqua, ma puoi anche andare orizzontalmente fino a C e poi verticalmente fino a B.
Oppure puoi percorrere la verticale AE e poi la linea orizzontale EB.
Se devi disegnare la linea AB in Scala 3 : 1, a partire da A ti sposti di 9 quadretti in orizzontale a destra e 6 quadretti in verticale verso il basso e arrivi in B; poi unisci AB con una linea.
Si può dire che la linea obliqua AB è formata da due componenti: una orizzontale (3 quadretti) e una verticale (2 quadretti). Nelle DEFORMAZIONI, le due componenti vengono trattate diversamente: una segue la Scala verticale e l'altra la Scala orizzontale.
In questo caso la componente verticale viene dimezzata (Scala 1 : 2), 1 quadretto anziché 2, mentre la componente orizzontale resta invariata, 3 quadretti (Scala 1: 1)
Qui la componente verticale raddoppia (Scala 2 : 1) e quella orizzontale dimezza (Scala 1 : 2).
Esercizio 1
Esercizio 1




















fantastico per spiegare il reticolo geografico
RispondiEliminacarta di Peters e/ Marcatore