LE ROTAZIONI
Le ROTAZIONI fanno parte delle TRASFORMAZIONI GEOMETRICHE e appartengono alle ISOMETRIE (vedi Simmetria assiale).
Una TRASFORMAZIONE GEOMETRICA tra i punti del piano è una corrispondenza biunivoca che ad ogni punto P del piano associa uno e uno solo punto P' appartenente al piano stesso e viceversa. (Un po' complicato...fra qualche anno ti sarà più chiaro)
Per semplificare: Un punto P della figura iniziale, dopo la trasformazione corrisponde ad un altro punto P' del piano stesso e questo punto P' viene detto IMMAGINE di P.
Per effettuare una rotazione è necessario stabilire un CENTRO DI ROTAZIONE, un ANGOLO DI ROTAZIONE e il verso ORARIO o ANTIORARIO.
La rotazione trasforma una figura geometrica in una figura (immagine) congruente a quella data.
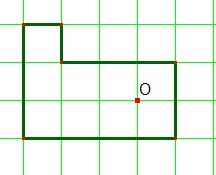
Il centro di rotazione può anche essere un punto interno alla figura. Funziona come un chiodo attorno al quale si fa girare la figura tanto quanto indicato dall'angolo di rotazione.
Si abbia questo poligono, il centro di rotazione O, si effettui la rotazione di 90° in senso orario.
Se effettui un'altra rotazione di 90° in senso orario.
E ancora una rotazione di 90° in senso orario.
Si può osservare che:
la rotazione di 90° in senso orario equivale alla rotazione di 270° in senso antiorario;
la rotazione di 180° in senso orario e senso antiorario sono equivalenti;
la rotazione di 90° in senso antiorario equivale alla rotazione di 270° in senso orario.
Vediamo ora come si costruisce una rotazione su un foglio quadrettato.
In questa lezione si considerano solo le rotazioni di 90°, 180° e 270°.
Sia O il centro di rotazione e si voglia ruotare il punto A di 90° in senso orario.
Se A si trova sulla stessa linea orizzontale di O, basta tracciare la perpendicolare (linea verticale) per O e considerare la distanza AO = A'O.
Sia O il centro di rotazione e si voglia ruotare A di 90° in senso antiorario.
Se A si trova sulla stessa linea verticale di O, traccia la linea perpendicolare (orizzontale) per O e considera la distanza AO = A'O.
Sia O il centro di rotazione, si ruoti A di 90°
Il punto A sta sulla stessa diagonale (ai quadretti) di O.
Traccia la diagonale ai quadretti perpendicolare, passante per O. Il punto A' si trova alla stessa distanza A da O, misurato sulle diagonali. AO = A'O.
Con centro di rotazione O, ruota A di 180° in senso orario.
Se A sta sulla retta orizzontale o verticale, passante per O, anche A' sta sulla stessa retta, alla stessa distanza da O. AO = A'O
Ruota di 180° il punto A, con centro di rotazione O.
Se A sta sulla diagonale passante per O, anche A' sta sulla stessa diagonale, alla stessa distanza da O. AO = A'O
Esercizio 1
Ruota la figura di 90° in senso orario essendo O il centro di rotazione.
Come vedi i punti A, E si trovano sulla stessa diagonale ai quadretti di O. Disegna la diagonale perpendicolare passante per O e riporta AO = A'O ; EO = E'O.
A questo punto non è il caso di considerare gli altri vertici della figura perché è semplice costruire la figura ruotata.
Esercizio 2
Ruota la figura di 90° in senso orario essendo O il centro di rotazione.
Come vedi i punti A e B sono sulla verticale passante per O, il punto C sulla diagonale passante per O.
Costruisci i punti immagine A', B', C' (secondo quanto detto sopra).
Siccome la figura ruotata si sovrappone all'altra, noi la disegniamo separata riportando il centro O di rotazione.
Anche i punti E, F si trovano sulla diagonale passante per O.
Costruisci i punti immagine F' e E'. FO = F'O , EO = E'O
A questo punto si riesce a disegnare la figura ruotata senza considerare altri vertici.
Esercizio 3
Ruota la figura di 90° in senso orario, di 180° in senso orario, di 270° in senso orario, con centro di rotazione O.
In questo caso è facile disegnare la figura ruotata, senza dover costruire le immagini di alcuni vertici.
Esercizio 4
Ruota la figura di 90° in senso antiorario, di 90° in senso orario, di 180° in senso antiorario, con centro di rotazione O.
Esercizio 5
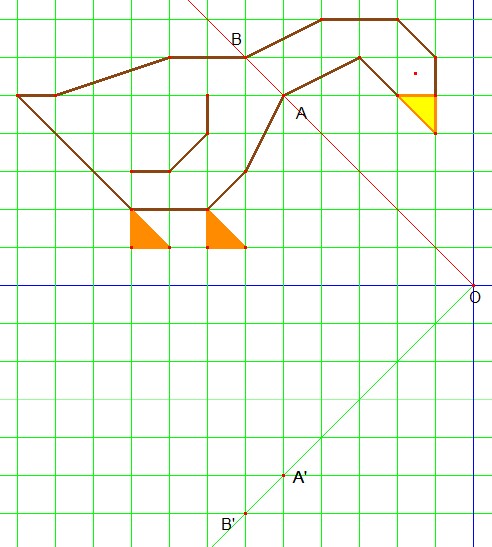
Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
Considera i punti A, B, C, allineati sulla verticale che passa per O.
Costruisci i punti immagine A', B', C'.
Poi (con la logica) completa la rotazione.
Esercizio 6
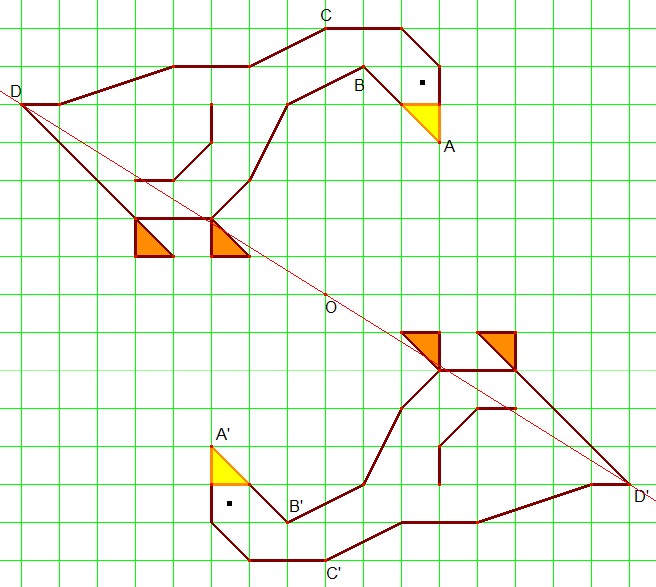
Ruota la figura di 180° in senso antiorario, con centro di rotazione O.
Come vedi i punti A, B, C sono allineati sulla stessa retta diagonale passante per O. I punti E, D sulla orizzontale passante per O.
Costruisci i punti immagine A', B', C', D', E'.
Poi completa la figura ruotata.
Esercizio 7
Ruota la figura di 90° in senso orario, con centro di rotazione O.
Ruota l'immagine di 180° in senso orario con centro di rotazione O.
Esercizio 8
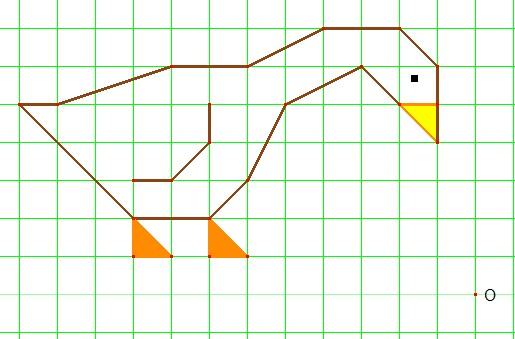
Ruota la figura di 90° in senso orario con centro di rotazione O.
Esercizio 9
Ruota la figura di 180° in senso antiorario, con centro di rotazione O.
Esercizio 10
Ruota di 90° in senso orario con centro di rotazione O.
APPROFONDIMENTI
Ruota il punto A di 90°.
Questo punto non sta sulla diagonale passante per O e nemmeno sulla verticale o sull'orizzontale.
Considera che A dista da O 2q in verticale e 3q in orizzontale e il percorso è una L (elle).
Per effettuare la rotazione di A di 90° in senso orario basta ruotare questa L di 90°.
Per ruotare A di 90° in senso antiorario ruota la L di 90°in senso antiorario.
Per ruotare A di 180° ruota sempre la L di 180°.
Puoi notare che nella rotazione di 180° i punti A e A' appartengono alla stessa retta che passa per O.
Rotazione di A di 90° in senso antiorario
1) Ruota la figura di 90° in senso orario, con centro di rotazione O.
Il punto A sta sulla verticale passante per O, cominciamo a ruotare questo punto.
Scegliamo un altro punto caratteristico della figura, esempio d, ed effettuiamo la rotazione.
Procediamo allo stesso modo con un altro punto (esempio C).
A questo punto, considerando A', B' e C' è possibili costruire la figura ruotata.
2) Ruota la figura di 90° in senso antiorario con centro di rotazione O.
I punti A e B su trovano sulla diagonale ai quadretti passante per O.
Considera la rotazione del punto C.
A questo punto potresti già costruire la figura ruotata, oppure puoi ancora considerare un altro punto (es. D).
Ora puoi costruire la figura ruotata.
3) Ruota la figura di 180° in senso orario, con centro di rotazione O.
Ruota il punto A di 180°.
Ruota B di 180°.
Ruota C, che si trova sulla verticale passante per O.
Verifica che il punto D e D' appartengono alla stessa retta passante per O.
4) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
Verifica che F e F' appartengono alla stessa retta passante per O.
6) Ruota la figura di 90° in senso orario, con centro di rotazione O.
7) Ruota la figura di 180° in senso antiorario, con centro di rotazione O.
8) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
9) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
10) Ruota la figura di 180° in senso orario, con centro di rotazione O.
Verifica che D e D' appartengono alla stessa retta passante per O.
11) Ruota la figura di 90° in senso orario, con centro di rotazione O.
13) Ruota la figura di 180°, con centro di rotazione O.
14) Ruota la figura di 90° in senso orario, con centro di rotazione O.
15) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
Considera che A dista da O 2q in verticale e 3q in orizzontale e il percorso è una L (elle).
Per effettuare la rotazione di A di 90° in senso orario basta ruotare questa L di 90°.
Per ruotare A di 90° in senso antiorario ruota la L di 90°in senso antiorario.
Per ruotare A di 180° ruota sempre la L di 180°.
Puoi notare che nella rotazione di 180° i punti A e A' appartengono alla stessa retta che passa per O.
Rotazione di A di 90° in senso antiorario
ESERCIZI
1) Ruota la figura di 90° in senso orario, con centro di rotazione O.
Il punto A sta sulla verticale passante per O, cominciamo a ruotare questo punto.
Scegliamo un altro punto caratteristico della figura, esempio d, ed effettuiamo la rotazione.
Procediamo allo stesso modo con un altro punto (esempio C).
A questo punto, considerando A', B' e C' è possibili costruire la figura ruotata.
2) Ruota la figura di 90° in senso antiorario con centro di rotazione O.
I punti A e B su trovano sulla diagonale ai quadretti passante per O.
Considera la rotazione del punto C.
A questo punto potresti già costruire la figura ruotata, oppure puoi ancora considerare un altro punto (es. D).
Ora puoi costruire la figura ruotata.
3) Ruota la figura di 180° in senso orario, con centro di rotazione O.
Ruota il punto A di 180°.
Ruota B di 180°.
Ruota C, che si trova sulla verticale passante per O.
Verifica che il punto D e D' appartengono alla stessa retta passante per O.
4) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
5) Ruota la figura di 180° in senso antiorario, con centro di rotazione O.
Verifica che F e F' appartengono alla stessa retta passante per O.
6) Ruota la figura di 90° in senso orario, con centro di rotazione O.
7) Ruota la figura di 180° in senso antiorario, con centro di rotazione O.
8) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
9) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
10) Ruota la figura di 180° in senso orario, con centro di rotazione O.
Verifica che D e D' appartengono alla stessa retta passante per O.
11) Ruota la figura di 90° in senso orario, con centro di rotazione O.
12) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.
13) Ruota la figura di 180°, con centro di rotazione O.
14) Ruota la figura di 90° in senso orario, con centro di rotazione O.
15) Ruota la figura di 90° in senso antiorario, con centro di rotazione O.














































































































Mm o
RispondiEliminaBellissima pagina!👍🏻😊
RispondiElimina