Immagina che i lati delle figure siano delle aste senza spessore legate fra loro con dei perni. Mantenendo fermo un vertice (perno) si possono spostare gli altri ottenendo figure deformate o trasformate.
La definizione di trasformazione geometrica è un po' complessa:
1) In generale per trasformazione geometrica si intende un qualsiasi procedimento che permette di ottenere da una figura data F un’altra F’ i cui punti sono in corrispondenza biunivoca con quella data.
2) Una trasformazione geometrica (t) tra i punti di un piano è una funzione che fa corrispondere ai punti del piano altri punti del piano stesso e viceversa (trasformazione biunivoca)
La definizione di trasformazione geometrica è un po' complessa:
2) Una trasformazione geometrica (t) tra i punti di un piano è una funzione che fa corrispondere ai punti del piano altri punti del piano stesso e viceversa (trasformazione biunivoca)
trasformazione QUADRATO-ROMBO
Costruisci un quadrato di lato AB (5 cm)
Traccia il lato AB e costruisci la perpendicolare per A.
Con la stessa apertura di compasso (AB) punta in D, traccia un arco, poi punta in B e traccia l'arco che taglia il precedente in C.
Immagina ora di mantenere fermo il vertice A e di spostare C e D. Questi seguiranno l'arco A-D.
Sposta D in E (a tuo piacere) e B in F (a tuo piacere).
Traccia la perpendicolare passante per A-1. Punta il compasso in O, con apertura OA, traccia l'arco in G.
(Il rombo ha le diagonali perpendicolari che si intersecano nel loro punto medio).
Unisci AFGE, vertici del rombo che ha i lati della stessa lunghezza di quelli del quadrato ABCD.
Dal quadrato ABCD si possono ottenere infiniti rombi con i lati della stessa lunghezza.
Se sposti i vertici D in E, B in F, ottieni il rombo:
Se non sposti D e sposti B in F ottieni il rombo AFGD:
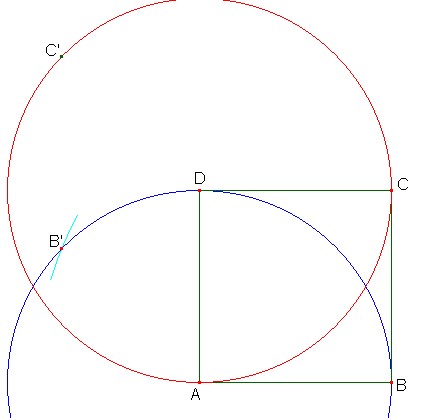
A partire dal quadrato ABCD, mantieni fissi i vertici A, D e sposta a tuo piacere i vertici B, C.
Il vertice B si sposta sulla circonferenza blu e il vertice C si sposta sulla circonferenza rossa.
Sposta C in C' (a tuo piacere)
Spostando C anche B si sposta e per individuare la sua posizione devi aprire il compasso C-C', puntare in B e intersecare la circonferenza blu in B'.
Unisci AB'C'D, vertici del rombo ottenuto dalla trasformazione del quadrato ABCD.
Se sposti il vertice C in C', apri il compasso C-C', punta in B, taglia la circonferenza blu in B'.
Unisci AB'C'D, vertici del rombo ottenuto dalla trasformazione del quadrato ABCD.
Se sposti il vertice C in C', apri il compasso C-C', punta in B, taglia la circonferenza blu in B'.
Unisci AB'C'D, vertici del rombo ottenuto dalla trasformazione del quadrato ABCD.
Mantenendo fisso il lato AD del quadrato, si ottengono, per trasformazione, infiniti rombi.
A partire dal quadrato ABCD, mantieni fisso il vertice A e sposta verso l'esterno il vertice C.
Costruisci il quadrato ABCD e immagina di spostare C in C'.
Con apertura di compasso AB, traccia l'arco B-D. I vertici B e D potranno spostarsi solo su questo arco perché la loro distanza da A deve essere costante.
Traccia il segmento AC' (diagonale del rombo).
Apri il compasso esattamente quanto il lato del quadrato, punta in C', traccia l'arco che taglia il precedente in D' e B'.
Unisci i punti AB'C'D', vertici del rombo ottenuto dalla deformazione del quadrato ABCD.
A partire dal quadrato ABCD, mantieni fisso il vertice A e sposta verso l'interno il vertice C.
Costruisci il quadrato ABCD e immagina di spostare il vertice C in C'.
Con apertura di compasso AB, traccia l'arco B-D. I vertici B e D si possono spostare solo su questo arco perché devono mantenere costante la distanza da A.
Traccia il segmento AC, diagonale del rombo.
Con apertura di compasso uguale al lato del quadrato, punta in C', traccia l'arco che taglia il precedente in B' e D'.
Unisci AB'C'D', vertici del rombo ottenuto dalla deformazione del quadrato ABCD.
Nessun commento:
Posta un commento